電気の基礎理論
解答・解説
 lx
lx
読み方はルクス。
それぞれF(ファラド)は静電容量、lm(ルーメン)は光束、H(ヘンリー)はインダクタンスの単位です。
解答・解説
 8
8
2つの導体を比べるとき、導体の長さが2倍になると電気抵抗も2倍になります。
次に導体の直径または半径が2倍になると電気抵抗は4分の1になります。
これよりAはBより2倍の長さがあるため電気抵抗は2倍、またAはBに比べ直径が半分のため電気抵抗は4倍。
合わせて電気抵抗が8倍高くなります。
解答・解説
 32
32
導体の直径または半径が2倍になると電気抵抗は4分の1になります。
両方の軟銅線の電気抵抗を等しくするためには、長さが4倍でなければいけません。
8×4=32
解答・解説
 断面積5.5[mm2]、長さ10[m]
断面積5.5[mm2]、長さ10[m]
直径2.6mmの銅導線の断面積は、半径×半径×円周率で求められます。
1.3 × 1.3 × 3.14 ≒ 5.3
長さも等しいことからロ。
[イ]の断面積は、0.8×0.8×3.14≒2.0
[ハ]の断面積は、1.6×1.6×3.14≒8.0
電気抵抗は断面積と反比例し、長さに比例するため、問題の直径2.6mm、長さ10mの銅銅線の抵抗値を基準とすると、
[イ]断面積2.0÷5.3≒0.38 長さ20÷10=2 抵抗値2÷0.38=5.26倍
[ロ]断面積5.5÷5.3≒1.04 長さ10÷10=1 抵抗値1÷1.04=0.96倍
[ハ]断面積8.0÷5.3≒1.50 長さ5÷10=0.5 抵抗値0.5÷1.5=0.33倍
[ニ] 断面積8.0÷5.3≒1.50 長さ10÷10=1 抵抗値1÷1.5=0.66倍
抵抗値が最も近い値の[ロ]を選びます。
解答・解説
 2160
2160
電力量は、消費電力 × 時間 で表せます。
300W × 2時間 = 600W(h)
1秒間で1W=1Jのため、1W(h)=3600J
600W × 3600J = 2,160,000J = 2,160kJ となります。
解答・解説
 1.4
1.4
必要な熱量を求めます。
4.2kJ× 60l × 20℃ = 5040
熱効率は100%なので、5040kJが必要な熱量です。
電力量は1秒1W = 1Jなので3600秒(1時間)で5040kJの熱量を出すために必要な電力量は
5040 / 3600 = 1.4
1.4kW(h)になります。
解答・解説
 1.2
1.2
合成抵抗の計算は下記の方法で行います。
①並列つなぎの合成抵抗 (抵抗値×抵抗値)/(抵抗値+抵抗値)
②直列つなぎの合成抵抗 抵抗値+抵抗値
この場合、並列の合成抵抗と直列の合成抵抗に分けて考えます。
回路下部の3Ωは直列なので 3 + 3 = 6Ω
回路上部の3Ωは並列なので(3×3)/(3+3) = 1.5Ω
これらを並列の合成抵抗と考えて (6×1.5)/(6+1.5) = 1.2
1.2Ωになります。
解答・解説
 1.8
1.8
合成抵抗の計算は下記の方法で行います。
①並列つなぎの合成抵抗 (抵抗値×抵抗値)/(抵抗値+抵抗値)
②直列つなぎの合成抵抗 抵抗値+抵抗値
並列の合成抵抗と直列の合成抵抗に分けて考えます。
回路下部の並列部分は(3×3)/(3+3) = 1.5Ω
この合成抵抗と隣の抵抗を直列の合成抵抗と考えて
1.5 + 3 = 4.5Ω
回路上部と回路下部それぞれの抵抗を並列の合成抵抗と考えて
(3×4.5)/(3+4.5) = 1.8
1.8Ωになります。
解答・解説
 160
160
図中の×の地点で断線するとa-c間の抵抗は直列の合成抵抗になります。
オームの法則から電圧 ÷ 抵抗 = 電流
200 / 10+40(直列の合成抵抗) = 4
4Aの電流が流れています。
b-c間の電圧は間の抵抗から求めます。オームの法則から
電流 × 抵抗 = 電圧
4 × 40 = 160 160Vになります。
解答・解説
 80
80
この回路のインピーダンスを求めます。
インピーダンスZは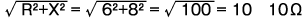 になります。
になります。
回路に流れる電流は Ⅰ=V/Z のため
100[V] ÷ 10[Ω] = 10 10
A
リアクタンスの電圧はオームの法則から
10[A] × 8[Ω] = 80 80Vになります。
解答・解説
 1
1
問題文の条件から電線に流れる電流を求めます。
I = P/V (P=消費電力、V=電圧) となるので
I = 2000/100 = 20 20Aになります。
次に電線の電気抵抗を求めます。
電線1000[m]の電気抵抗が3.2[Ω]なので
3.2/1000 = 0.0032 1mあたり0.0032Ωの電線が8mなので
0.0032 × 8 = 0.0256 0.0256Ωになります。
電圧降下を求める公式にこれらを代入します。
電圧降下を求める公式は 2rI なので
2 × 20 × 0.0256 = 1.024 約1Vになります。
解答・解説
 34
34
断面積5.5mm2の600Vビニル絶縁電線の許容電流は49Aです。
この問いの電流減少係数は0.7なので、49 × 0.7 = 34.3
答えは整数のため34.3 ≒ 34
| 単線 | より線 | ||
| 太さ | 許容電流値 | 総断面積 | 許容電流値 |
| 1.6mm | 27A | 2mm2 | 27A |
| 2.0mm | 35A | 3.5mm2 | 37A |
| 2.6mm | 48A | 5.5mm2 | 49A |
解答・解説
 24
24
直径2.0mmの600Vビニル絶縁電線の許容電流は35Aです。
この問いの電流減少係数は0.7なので、35 × 0.7 = 24.5
答えは整数のため24.5 ≒ 24
| 単線 | より線 | ||
| 太さ | 許容電流値 | 総断面積 | 許容電流値 |
| 1.6mm | 27A | 2mm2 | 27A |
| 2.0mm | 35A | 3.5mm2 | 37A |
| 2.6mm | 48A | 5.5mm2 | 49A |
解答・解説
 電気トースター
電気トースター
電気を熱に変える機械は力率が高くなります。
その他の例として電気コタツなどがあります。
解答・解説
 20
20
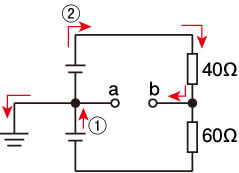
この回路に流れる電流は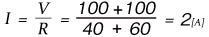
a点の電位は0[V](①から接地端子に流れるため)
②の電位は100[V]
②は40Ωの抵抗を通してbに流れるため、
2[A]×40[Ω]=80[V]
よってb点の電位は 100-80=20[V]
a-b間の電圧は20-0=20[V]
解答・解説
 7.2
7.2
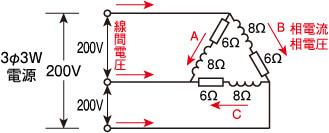
A,B,C各負荷のインピーダンスを求めます。
√(82+62)=√100=10Ω
Δ結線は線間電圧=相電圧なので、相電圧=200V
そのため、A,B,Cの各電流は200V / 10Ω=20A
次に、消費電力は相電圧×相電流×力率の公式を使います。
力率=抵抗R / インピーダンスZ=6 / 10=0.6
これを先ほどの公式に当てはめて、
200V×20A×0.6=2400W
これは負荷一個分の消費電力なので、3×2400W=7.2kW

